Die bekannten Kennzahlen Sharpe Ratio, Volatilität, Alpha, Beta oder Korrelation berücksichtigen konstruktionsbedingt nur Durchschnittsrenditen und Standardabweichungen von Wertpapierrenditen. Die Komplexität der Finanzmärkte lässt sich durch diese sparsame Dimensionierung dabei nur unzureichend darstellen.
Gleichzeitig erfordert die Messung und das Verwerten von Eigenschaften wie Renditeasymmetrien und sogenannter Fat Tails ein umfangreicheres theoretisches Gerüst. Allerdings geht dieses in der Regel mit Rechenaufwand und zusätzlichen Modellspezifikationen einher. Freunde der Generalisierung und Skeptiker rein akademischer Ansätze werden hiermit nur selten glücklich.
Weshalb ist es überhaupt so wichtig, über Durchschnittrenditen und Standardabweichungen hinauszugehen?
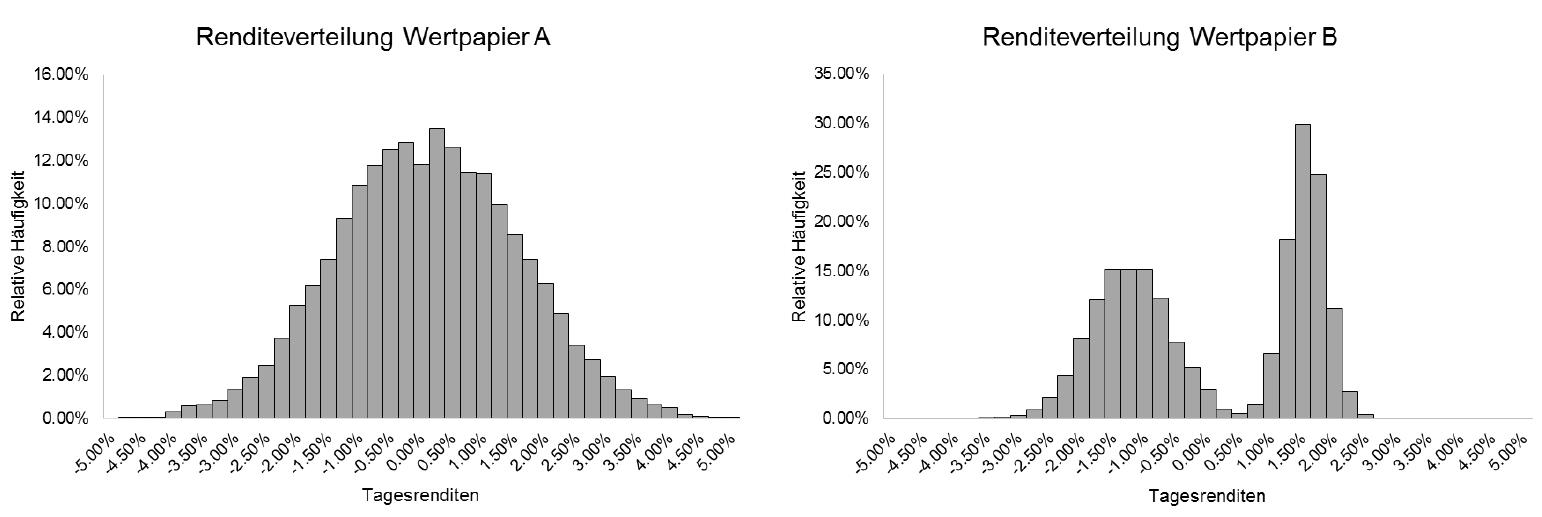
Die untenstehende Grafik illustriert das vorliegende Problem. Wertpapier A und Wertpapier B unterscheiden sich ganz offensichtlich in ihrem Rendite- und Risikoprofil. Während die Tagesrenditen von Wertpapier A um einen Mittelwert schwanken, realisieren sich Wertänderungen für Wertpapier B entweder um den Bereich von minus 1 oder plus 2 Prozent.
Ein solches Verhalten könnte man von einem Derivate-Portfolio erwarten. Nun kommt die Krux: Beide Wertpapiere haben die gleiche Durchschnittsrendite und Volatilität und damit beide auch eine identische Sharpe Ratio.
>>Vergrößern
Eine ähnliche Grafik zeigten die Wissenschaftler Con Keating und William Shadwick Anfang 2002 bei der Präsentation der von ihnen erarbeiteten Omega Ratio. Diese Ratio geht einen anderen Weg und setzt die Renditen über einem bestimmten Wert (in der Regel null) in ein Verhältnis zu den Renditen unter diesem Schwellwert.
>>Vergrößern

Hierbei geht es nicht nur um die schiere Anzahl dieser Punkte, sondern auch um deren Ausprägung. So wird ein absoluter Gewinn oder Verlust mit seiner historischen Häufigkeit verrechnet und dann entweder in den Zähler (Gewinn) oder Nenner (Verlust) gesteckt.
Am Ende ist dieses Vorgehen nichts anderes als eine Renditeverteilung in der Mitte zu teilen und die positive Seite durch die negative zu teilen. Ist die linke Seite also entweder durch Häufigkeit oder extreme Höhe von Verlusten überproportional groß, fällt die Omega Ratio unter 1. Überwiegen allerdings die Gewinnchancen auf der rechten Seite, steigt die Kennzahl an.
Da die Ratio direkt aus der empirischen Verteilung errechnet wird, enthält sie auf natürliche Art und Weise Informationen zu Schiefe sowie den Fat Tails und hört nicht bei der Standardabweichung auf.
Gleichzeitig erfordert die Messung und das Verwerten von Eigenschaften wie Renditeasymmetrien und sogenannter Fat Tails ein umfangreicheres theoretisches Gerüst. Allerdings geht dieses in der Regel mit Rechenaufwand und zusätzlichen Modellspezifikationen einher. Freunde der Generalisierung und Skeptiker rein akademischer Ansätze werden hiermit nur selten glücklich.
Weshalb ist es überhaupt so wichtig, über Durchschnittrenditen und Standardabweichungen hinauszugehen?
Die untenstehende Grafik illustriert das vorliegende Problem. Wertpapier A und Wertpapier B unterscheiden sich ganz offensichtlich in ihrem Rendite- und Risikoprofil. Während die Tagesrenditen von Wertpapier A um einen Mittelwert schwanken, realisieren sich Wertänderungen für Wertpapier B entweder um den Bereich von minus 1 oder plus 2 Prozent.
Ein solches Verhalten könnte man von einem Derivate-Portfolio erwarten. Nun kommt die Krux: Beide Wertpapiere haben die gleiche Durchschnittsrendite und Volatilität und damit beide auch eine identische Sharpe Ratio.
>>Vergrößern

Eine ähnliche Grafik zeigten die Wissenschaftler Con Keating und William Shadwick Anfang 2002 bei der Präsentation der von ihnen erarbeiteten Omega Ratio. Diese Ratio geht einen anderen Weg und setzt die Renditen über einem bestimmten Wert (in der Regel null) in ein Verhältnis zu den Renditen unter diesem Schwellwert.
>>Vergrößern

Hierbei geht es nicht nur um die schiere Anzahl dieser Punkte, sondern auch um deren Ausprägung. So wird ein absoluter Gewinn oder Verlust mit seiner historischen Häufigkeit verrechnet und dann entweder in den Zähler (Gewinn) oder Nenner (Verlust) gesteckt.
Am Ende ist dieses Vorgehen nichts anderes als eine Renditeverteilung in der Mitte zu teilen und die positive Seite durch die negative zu teilen. Ist die linke Seite also entweder durch Häufigkeit oder extreme Höhe von Verlusten überproportional groß, fällt die Omega Ratio unter 1. Überwiegen allerdings die Gewinnchancen auf der rechten Seite, steigt die Kennzahl an.
Da die Ratio direkt aus der empirischen Verteilung errechnet wird, enthält sie auf natürliche Art und Weise Informationen zu Schiefe sowie den Fat Tails und hört nicht bei der Standardabweichung auf.


